Today, we will explore how to use AI for correlation analysis to understand the relationships between variables. Don’t worry about using the AI Agent-driven Bayeslab; all you need is natural language to get the data analysis result.

We will start with a dataset named “XY: Correlation.csv,” focusing on three key weather variables and their relationship with ozone levels.

Correlation analysis involves examining two or more variables to determine the strength and direction of their relationship. Our steps will include:

Step 1 — Correlation Analysis: Through correlation analysis, we can identify the relationship between weather variables and ozone levels.

Step 2 — Scatter Plot: Create scatter plots to visualize how these variables interact with each other.

Today’s data source is a typical 2D data table structure, which is one of the six common table structures.

There are two main types of 2D data tables: One for Single Y-Value ,and the other for Multiple Replicate Y-Values

Type 1 :Single Y-Value Input

● Description:

○ Input each point with a single Y-value.

○ Each group’s data is stored in the respective column

● Suitable for:

○ Displaying and comparing data for different groups at a single time point.

Type 2 : Multiple Replicate Y-Values Input in Side by Side Subcolumns

● Description:

○ Input each point with Enter n replicate values in side-by-side subcolumns:

○ Multiple Y-values for each group are stored in respective columns.

● Suitable for:

○ Detailed recording multiple sets of data obtain from repeated measures at a single time point.

Today, we are using Type 1: Single Y-Value.

Each row consists of an X independent variable and its corresponding Y dependent variable.

Typically, we plot the X values on the X-axis and the Y values on the Y-axis.

We will introduce Multiple Replicate Y-Values later.

Step 1 — Correlation Analysis

First, the correlation analysis. Here is the language description: The general business requirement is to obtain three correlation coefficients showing how each weather variable relates to ozone levels.

Confidence level for the analysis is 95%, which is generally used.

Additional requirements include rounding the analysis results to a certain number of decimal places and tell AI that the raw data follows a normal distribution.

The analysis results shall be saved in the file named : Correlation Analysis.csv.

So let’s see the analysis result together.

So except all the requirements we mentioned above, we can also see whether the correlations are significant at the 95% confidence level.

According to our analysis we could reveal a strong positive correlation between sunlight duration and temperature with ozone levels, while humidity shows a negative correlation.

Next, if we plot a scatter plot, it will visually confirm these relationships by showing how each variable’s data points relate to ozone levels.

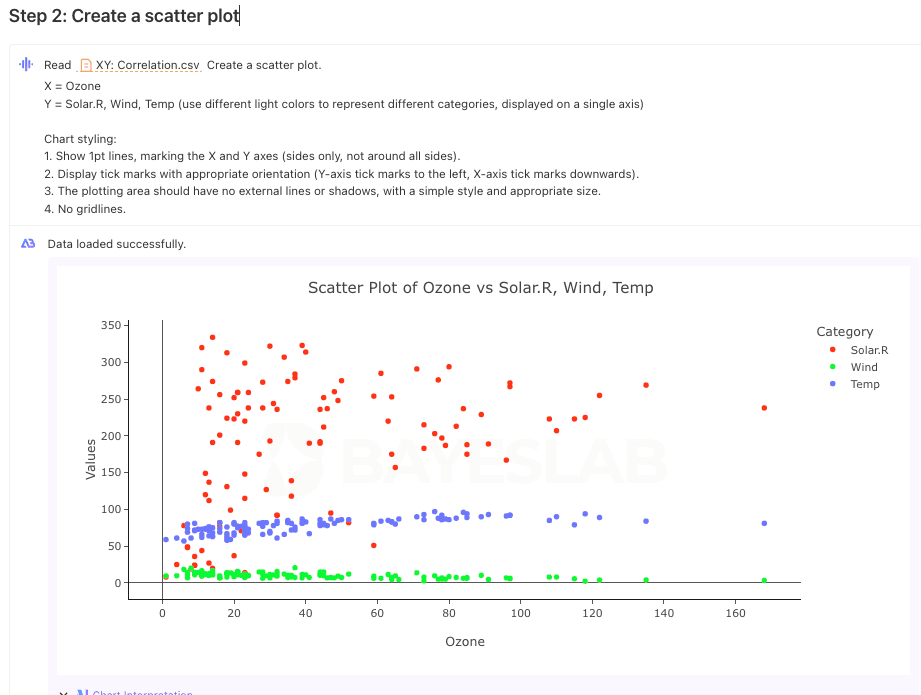
Step 2 — Scatter Plot

Again, here we are referring to the prompt :

X = Ozone

Y = Solar.R, Wind, Temp

Use different light colors to represent different categories, displayed on a single axis.

These main points are quite important. Additionally, I included a few small requests regarding chart aesthetics, as described below:

This way, we obtain the scatter plot we need.

Supplement:

Below are some minor details that may be helpful for understanding if necessary.

Correlation Analysis

● If the data follows a normal distribution, we’ll use the Pearson correlation coefficient. The correlation coefficient (r) ranges from -1 to +1.

● If the data does not follow a normal distribution, we would use the non-parametric Spearman correlation, which also ranges from -1 to +1.

In this case, since the data follows a normal distribution, we’ll use Pearson’s method.

Data Interpretation, Correlation Coefficient Values ((r) or (rs)):

● ( 1.0 ): Indicates a perfect positive correlation.

● ( 0 < r < 1 ): Indicates a positive relationship where variables increase or decrease together.

● ( 0.0 ): Indicates no correlation.

● ( -1 < r < 0 ): Indicates a negative relationship where one variable increases as the other decreases.

● ( -1.0 ): Indicates a perfect negative correlation.

Understanding the Correlation,If (r) or (rs) is far from zero, it can mean:

● Changes in variable X influence changes in variable Y.

● Changes in variable Y influence changes in variable X.

● A third variable might be affecting both X and Y.

● The observed strong correlation might be coincidental without a causal relationship.

P-Value:

The p-value helps quantify the likelihood of obtaining the observed correlation by chance. A low p-value typically indicates significant correlation.